角的平分线的性质定理四个要点|含典型例题解析

#初中数学##角的平分线##初中几何#
欧几里得在《几何原本》中对角如此描述:两条直线相交,如果不重合的话,一条直线相对于另一条直线的倾斜度叫角。由此我们可以理解角是对两条直线关系的刻画,本质是两条边张开幅度的大小。也可以理解为是线绕一个点旋转的动态呈情况。
来看知识要点
要点一、角的平分线的性质
1.角的平分线上的点到角两边的距离相等。
2.要点诠释:用符号语言表示角的平分线的性质定理为:若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF。

要点二、角的平分线的逆定理
1.角的内部到角两边距离相等的点在角的平分线上.
2.要点诠释:
用符号语言表示角的平分线的判定:
若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB

要点三、角的平分线的尺规作图
角平分线的尺规作图
(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.
(2)分别以D、E为圆心,大于1/2DE的长为半径画弧,两弧在∠AOB内部交于点C.
(3)画射线OC.

射线OC即为所求。
要点四、四种常考轨迹
1.把符合某些条件的所有点的集合叫做点的轨迹。
2.和线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
3.在一个角的内部(包括顶点)且到角两边距离相等的点的轨迹是这个角的平分线.
4.到定点的距离等于定长的点的轨迹是以这个定点为圆心,定长为半径的圆.
来看例题精讲
类型一、角的平分线的性质及判定
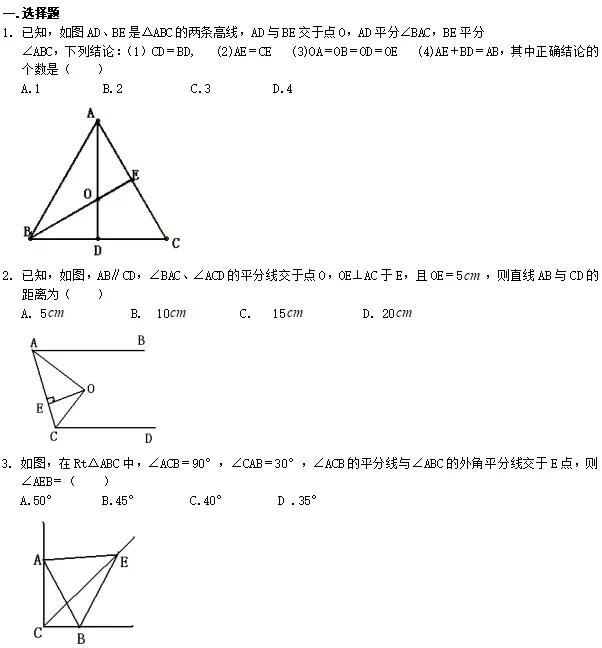
例1、已知:如图,在ΔABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F.求证:AE=AF.

解析:

总结:先由角平分线的性质得出DE=DF,再证ΔAED≌ΔAFD,即可得出AE=AF.分析已知,寻找条件,顺次证明.
试一试:如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于点E,DF⊥AC于点F,且DB=DC.求证:BE=CF.
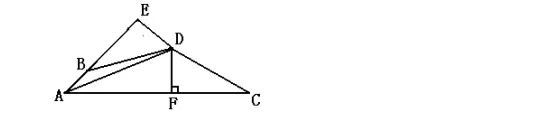
【答案】
证明:∵DE⊥AE,DF⊥AC,AD是∠BAC的平分线,∴DE=DF,∠BED=∠DFC=90°
在Rt△BDE与Rt△CDF中,DB=DC且DE=DF,
∴Rt△BDE≌Rt△CDF(HL)
∴BE=CF
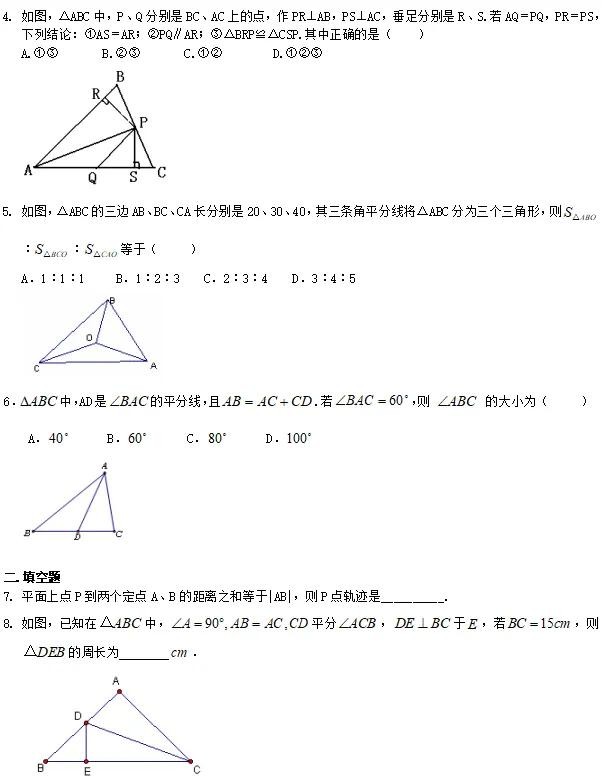
例2、如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为:( )
A.11 B.5.5 C.7 D.3.5
【答案】 B;

总结:本题求△EDF的面积不方便找底和高,利用全等三角形可用已知△ADG和△AED的 面积来表示△EDF面积.
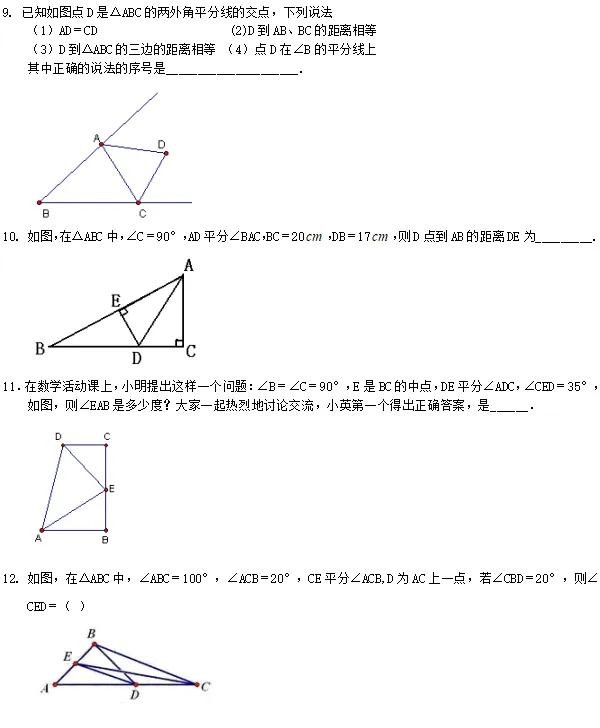
例3、如图,AC=DB,△PAC与△PBD的面积相等.求证:OP平分∠AOB.
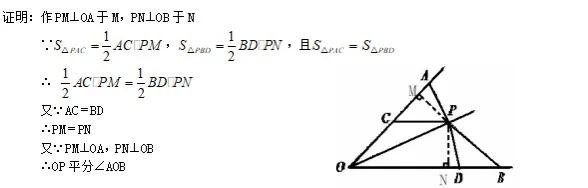
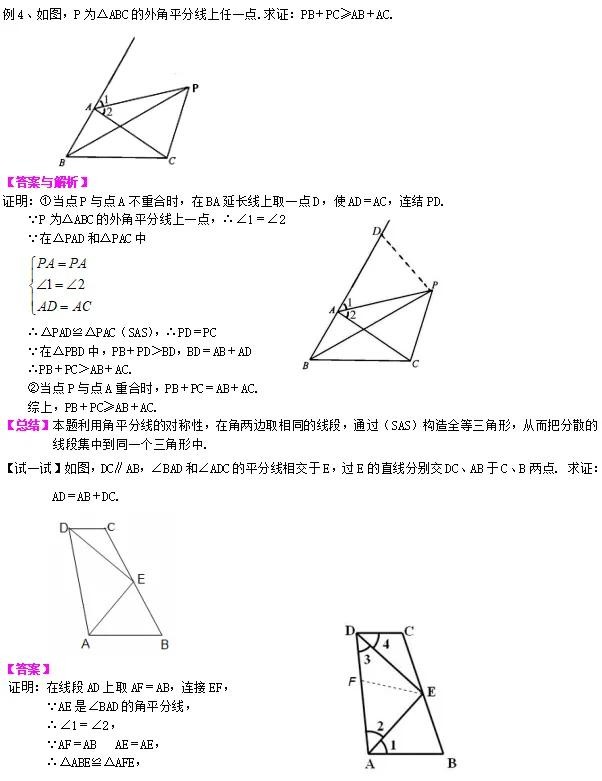
类型二、角的平分线的性质综合应用

类型三、点的轨迹
例5、到直线的距离等于2的点的轨迹是()
A.半径为2的圆
B.与l平行且到l的距离等于2的一条直线
C.与l平行且到l的距离等于2的两条直线
D.与l垂直的一条直线
【答案】C;到直线距离相等的点的集合是它的平行线,因为在直线两侧都可以做,所以有两条这样的直线.
总结:本题考查两平行线间的距离,两条这样的直线可能有些同学考虑不到,导致误选B.
最后来看下测试题: